Paylaşım TarihiKasım 28, 2024

Stratejik etkileşimlerin incelendiği bir matematiksel modelleme alanı olan oyun teorisi, birden fazla karar vericinin (oyuncuların) bir araya geldiği, her oyuncunun kendi çıkarları doğrultusunda kararlar aldığı durumları analiz etmek için kullanılan bir yaklaşımdır. Oyun teorisinde, her oyuncunun diğerlerinin ne yapacağını dikkate alarak kendi en iyi stratejisini belirlemeye çalıştığı varsayımı üzerinden hareket edilmektedir. Bu teori; ekonomi, siyaset bilimi, biyoloji, psikoloji gibi pek çok alanda uygulanmaktadır. Oyun teorisinde en bilinen denge türü, Nash dengesidir. Nash dengesinde hiçbir oyuncu, diğer oyuncuların stratejilerini değiştirmesi durumunda bile kendi stratejisini değiştirmeye gerek duymamaktadır.
Bilindiği üzere sürdürülebilirlik, bugünün ihtiyaçlarının gelecek nesillerin ihtiyaçlarını karşılama yeteneklerini tehlikeye atmadan karşılanmasını, bu çerçevede doğal kaynakların ve çevresel dengelerin korunmasını amaçlayan bir yaklaşımdır. Sürdürülebilirlik, ekonomik, çevresel ve sosyal boyutları olan bir kavramdır ve bu üç alan arasında dengeli bir ilişki kurmayı hedeflemektedir.
Sürdürülebilirlik ve oyun teorisi, yüzeyde farklı kavramlar gibi görünseler de, yakından bakıldığında bu iki kavramın birçok ortak noktaya sahip oldukları anlaşılmaktadır. Sürdürülebilirlik ve oyun teorisi, özellikle kaynakların yönetimi, çevre politikaları ve iş birliği gibi konular üzerinden birbirine bağlıdır. Oyun teorisi, birden fazla aktörün olduğu durumlarda kararların sonuçlarını modellemeyi sağlamaktadır. Teoriye göre aktörler, çıkarlarını maksimize etmek için çeşitli stratejiler geliştirebilmektedir. Benzer şekilde, sürdürülebilirlik hedeflerine ulaşmak için de farklı aktörler (devletler, şirketler, bireyler) arasında bir denge kurmak gereklidir.
Oyun teorisi, ortaya çıkan ya da çıkması muhtemel olan çatışmaları ve iş birliği fırsatlarını anlamada güçlü bir araçtır. Örneğin iki taraf, kısa vadede bireysel çıkarlarını maksimize etmek için iş birliği yapmaktan kaçınırsa, her iki taraf da uzun vadede olumsuz sonuçlarla karşılaşabilir. Sürdürülebilirlikte de benzer bir kritik denge vardır; ülkeler veya şirketler kaynakları aşırı tüketerek kısa vadede ekonomik çıkarlarını maksimize edebilirler. Ancak bu durum, uzun vadede çevresel tahribat ve kaynak kıtlığına yol açar, bu da belli bir aşamadan sonra ekonomik katma değerin azalmasına/sınırlanmasına sebep olur. Bu yüzden, kısa vadeli bireysel çıkarlar ile uzun vadeli kolektif fayda arasında bir denge kurmak gerekmektedir.
Tek seferlik oyunlarda, bireyler genellikle kendi çıkarlarını maksimize etmeye çalışırlar ve bu durum dezavantajlı (bir yönüyle sürdürülemez) sonuçlar doğurabilir. Ancak oyun tekrarlandığında, aktörler uzun vadeli kazançları göz önünde bulundurmak zorunda kalırlar ve iş birliği yapma eğiliminde olurlar. Bu da sürdürülebilirlik için önemli bir faktördür: uzun vadeli düşünme ve iş birliği, doğal kaynakların korunması ve çevresel bozulmanın önlenmesi için kritik rol oynamaktadır.
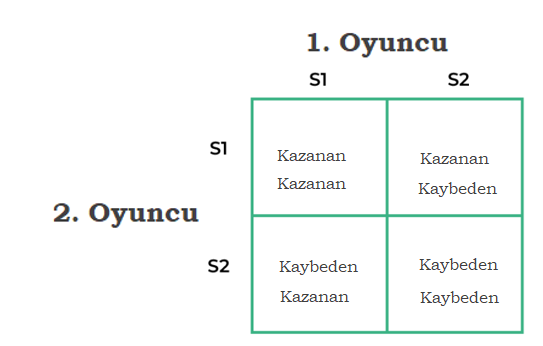
Aşağıdaki tabloda da belirtildiği gibi iki oyuncunun da birbirinin yaklaşımını bildiği ya da yaklaşımının farkına vardığı ve her ikisinin de başlangıç stratejisini uygulayacağı durumu göz önüne aldığımızda, S1 stratejisi en uygun strateji olacaktır. Çünkü oyuncular, bu stratejiden sapmanın oyunun çıkarına uygun olmayacağını bilirler. S1’i seçmeleri durumunda, her iki oyuncu da kazanacaktır. Diğer durumlarda ise, S2’ye sapmaları ikisinden birinin veya ikisinin yenilgisiyle sonuçlanacaktır.1
Oyun Teorisi Modelleri ve Sürdürülebilirlik
- Mahkumlar İkilemi (Prisoner’s Dilemma): Mahkumlar İkilemi, oyun teorisinin en ünlü ve klasik problemlerinden birisidir. İki suçlunun yakalanıp ayrı hücrelere konulduğu bir senaryoya dayanır ve stratejik karar almanın analizini yapar. İki suçlunun, birbirleriyle iletişim kuramadan, kişisel çıkarları doğrultusunda karar vermesi gereken bir senaryo üzerinden mesele anlatılır. Bu örnekte iki mahkum (A ve B) ciddi bir suçtan dolayı yakalanır, ancak polis onları suçlu gösterecek yeterli delile sahip değildir. Bu yüzden, onları ayrı hücrelere koyar ve her birine şu teklifi yapar:2
- Her ikisi de suçlamazsa (sessiz kalırsa): Her ikisi de küçük bir suçtan dolayı 1 yıl hapis cezası alacaktır.
- Birisi diğerini suçlarsa (itiraf ederse), ancak diğeri sessiz kalırsa: İtiraf eden serbest kalacak, ancak diğer suçlu 10 yıl hapis cezası alacaktır.
- Her iki mahkum da birbirini suçlarsa (itiraf ederlerse): Her ikisi de 5 yıl hapis cezası alacaktır.
Karar Durumları:
- Her ikisi de sessiz kalır: 1 yıl hapis (en iyi ortak sonuç).
- Birisi itiraf eder, diğeri sessiz kalır: İtiraf eden serbest kalır, diğeri 10 yıl hapis yatar.
- Her ikisi de itiraf ederse: Her ikisi de 5 yıl hapis cezası alır (ikisi için de orta bir sonuç).
İkilem:
İki mahkum da birbirinin kararını bilmeden hareket etmek zorundadır. Her mahkum, eğer diğerinin itiraf edeceğini düşünürse, en iyi seçenek kendisinin de itiraf etmesidir (çünkü diğerinin sessiz kalması durumunda serbest kalma şansı vardır). Ancak, iki taraf da aynı şekilde düşünür ve itiraf ederse, her ikisi de 5 yıl hapis yatar.
Bu durumda, her iki mahkumun en rasyonel stratejisi itiraf etmek gibi görünse de, aslında işbirliği yapıp sessiz kalsalardı, sadece 1 yıl hapis cezası alacaklardı. Ancak güven eksikliği ve karşı tarafın kararından emin olamamak, onları iş birliği yapmaktan alıkoyar. Böylece, bireysel çıkarlar, toplu çıkarlarla çatışır.
İkilemin temelinde, bireylerin çıkarlarının çatıştığı bir durumda nasıl karar verdikleri sorusu yatar. Mahkumlar İkilemi, sürdürülebilirlik ile doğrudan ilişkili bir oyun teorisi senaryosudur. İki taraf, iş birliği yaparak uzun vadede daha iyi bir sonuç elde edebilir.
Bireysel kısa vadeli çıkarlar, tarafların sürdürülebilirlik açısından zararlı kararlar almasına neden olabilir. Örneğin, şirketler çevresel konularda sorumluluk almazlarsa, kısa vadede kar elde edebilirler, ancak uzun vadede çevresel bozulmalarla karşı karşıya kalabilirler ve bu da onların karını/istikrarını olumsuz yönde etkileyebilir.
- Ortak Malların Trajedisi (Tragedy of the Commons): Bu teori, ortak malların özel mülkiyete konu edilmemesi durumunda ortaya bir trajedi çıkacağını, bu felâketin en dip sebebinin ise nüfus artışı olduğunu dile getirmiştir. Bu konu ile alakalı Hardin’in3 “Tragedy of Commons” (Ortak Malların/Kaynakların Trajedisi) adlı makalesinde, ortak malların özel mülkiyete konu edilmemesi durumunda ortaya bir trajedi çıkacağını, bu felâketin en dip sebebinin ise nüfus artışı olduğu dile getirilmektedir.
Bu konuya örnek olarak bir köydeki çiftçilerin ortak bir otlak alanını kullandığını düşünelim. Her çiftçi, kendi hayvanlarını otlatmak için bu alanı kullanır. Her bir çiftçi, daha fazla hayvan otlatmanın kendisi için faydalı olduğunu düşünür, çünkü kısa vadede kazanç sağlar. Ancak herkes bu şekilde düşünürse, otlak aşırı kullanılır ve sonunda verimsiz hale gelir. Bu da tüm köylülerin hayvanlarını besleyememesi anlamına gelir. Bu durum, bireysel kısa vadeli çıkarlar ile toplu uzun vadeli çıkarlar arasındaki çatışmayı gösterir.
Oyun teorisi bağlamında, bireylerin rasyonel olarak hareket edip kendi çıkarlarını maksimize etmeleri durumunda, sürdürülebilir olmayan bir tüketim standardının ortaya çıkması muhtemeldir. Bu ise, aşırı balıkçılık nedeniyle deniz türlerinin yok olması, duyarsız altyapı projeleriyle nedeniyle biyoçeşitliliğin tehlikeye girmesi, bilinçsiz ağaç kesimi nedeniyle ormansızlaşma veya kıymetli cevher/maden rezervlerinin süratle tükenmesi gibi çevresel sürdürülebilirlik sorunlarına yol açabilmektedir.
- Kamu Malları Oyunu (Public Goods Game): Tüketim açısından rakipli olmayan mallara “kamu malı” denir. Bunun en bilinen örneği deniz feneridir. Bir deniz feneri işaret ışığını yaktığı zaman, o ışığı gören bütün gemiler bundan istifade ederler. Herhangi bir müşterinin (geminin) bu ışığı almasıyla sağladığı kazanç (yolunu bulması), başkasının aynı anda bu hizmetten yararlanmasına engel olmaz.4 Neyin kamu malı olduğunun sınıflandırılması, çok kesin biçimde yapılabilecek bir iş değildir. Bu, biraz piyasa şartları ile teknolojik gelişmelere de bağlıdır. Gemide özel bir alıcı bulunmadıkça deniz fenerinden gönderilen sinyalleri almayı engelleyen bir sinyal bozucu cihaz icat edildiğini ve sinyale ulaşmaya yarayan özel alıcının da parayla satıldığını düşünelim. Bu durumda dışlanabilirlik ilkesi devreye girecek ve deniz feneri artık hâlis bir kamu malı olmaktan çıkacaktır. Kamu malı tarifinin bir şartını (dışlanabilir veya rakipli olmama) yerine getirip diğerini yerine getirmeyen bu türden mallara “hâlis olmayan kamu malları” denir ki, kamu mallarının pek çoğu bu sınıfa girmektedir.
Bir mal hem rakipli değil hem de dışlanabilir değilse, o mal “hâlis kamu malı”dır. Bu, “herhangi bir kişiye kullanılışlı kılındığı kadar topluluğun bütün üyelerine de fayda sağlayan”5 bir maldır. Böyle bir mal topluluktaki herkes tarafından kolektif olarak tüketilir ve kullanımından dolayı bir kişiye özel fatura çıkarılması söz konusu değildir. Hâlis kamu malları için verilen klâsik örnek millî savunma harcamalarıdır. Bu harcamalarla sağlanan korunma bir kişinin ya da grubun değil bütün ülkenin huzur ve barışına katkı sağlamaktadır, yani alınan hizmet dışlanabilir değildir. Öte yandan, bir kişinin ya da grubun aldığı hizmet, başkalarının aldığı hizmeti (sözgelimi huzur ve güven duygusunu) etkilemez veya azaltmaz, dolayısıyla alınan hizmet rakipli de değildir. Benzer şekilde hâlis kamu malı olarak görülebilecek hizmetler arasında itfaiye hizmetleri, iç güvenlik hizmetleri, adalet hizmetleri sayılabilir.
Bu konu sürdürülebilirlik kapsamında ele alındığında iklim değişikliği ile mücadelede ülkelerin veya şirketlerin sergilediği davranışlar, bireylerin kamu mallarına yatırım yapma istekliliği ile benzeştirilebilir. Çoğu oyuncu (ülke, şirket veya birey) bir kamu malına katkıda bulunmak istemeyebilir, çünkü bu maldan bedavaya faydalanma eğilimindedir. Konu rekabet ve sürdürülebilirlik açısından ele alınırsa çoğu zaman, şirketler veya devletler arasındaki rekabetin, kaynakların aşırı tüketilmesine yol açtığı gözlenebilir.
Oyun teorisi, bu tür rekabetçi senaryoları modelleyerek aktörlerin iş birliği yapmalarını veya daha sürdürülebilir stratejiler geliştirmeleri için gerekli koşulları yaratmalarını sağlamaktadır. Örneğin, “Nehir Havzalarında Sürdürülebilir Gelişme İçin Bir Yöntem: Oyun Teorisi” çalışmasında bir nehir havzasında yer alan Büyükşehir Belediyesi ve küçük ölçekli bir sanayi yatırımcısı arasındaki stratejik karar verme sürecinin modellenmesi incelenmektedir. Mevcut durumu (Oyun I) ve ideal durumu (Oyun II) gösteren iki ödeme matriksi oluşturulmuştur. Birinci oyunda oyuncular çevre maliyetlerini dikkate almadan karar verirlerken, ikinci oyunda oyuncular çevre mevzuatını ve çevre maliyetlerini dikkate alarak hareket ederler. Oyunlar; iki kişili, oyuncular arasında iş birliğinin olmadığı, sıfır toplamlı olmayan, sonlu oyunlardır. Her iki oyunda da oyuncular için en iyi strateji çiftini gösteren Nash dengesi araştırılmıştır. Büyükşehir Belediyesi sanayinin aşağı havzada organize sanayi bölgelerinde geliştirilmesini istemektedir, ancak birinci oyunda sanayici yukarı havzada sanayi alanlarının dışında yer seçmektedir. Çevre maliyetlerinin dikkate alındığı ikinci oyunda ise, Nash dengelerine göre, sanayici Büyükşehir Belediyesi içerisinde altyapısı tamamlanmış bir organize sanayi bölgesini seçmektedir. Sonuç olarak, ikinci oyunda her iki oyuncunun da gelirleri artmakta ve aynı zamanda çevre korunabilmektedir.
Özet olarak söylenebilir ki oyun teorisi, sürdürülebilirlik ile ilgili karar alma süreçlerini anlamada değerli bir çerçeve sunar. Hem bireysel hem de toplumsal düzeyde sürdürülebilirlik hedeflerine ulaşmak, oyun teorisinin öngördüğü gibi, stratejik iş birliği ve uzun vadeli düşünmeyi gerektirir. Aktörlerin kısa vadeli bireysel kazançlardan ziyade uzun vadeli kolektif faydaya odaklanmaları, hem oyun teorisinin hem de sürdürülebilirliğin temel ilkeleriyle örtüşür. Bu bağlamda, sürdürülebilirlik ve oyun teorisi, bireylerin, kurumların ve devletlerin daha dengeli ve adil bir dünya yaratma yolunda nasıl stratejik kararlar alabileceklerini anlama açısından birbirini tamamlayan kavramlardır.
Kaynakça:
1) Axelrod, R. (1984). The Evolution of Cooperation, Basic Books, s.2-4A. Şu adresten erişilebilir: https://ee.stanford.edu/~hellman/Breakthrough/book/pdfs/axelrod.pdf. Son erişim tarihi: Kasım 2024.
2) Demirci, E. (2019). “Ulusal Yazında Oyun Teorisi Üzerine Genişletilmiş Bir Literatür Taraması”, Mehmet Akif Ersoy Üniversitesi Sosyal Bilimler Enstitüsü Dergisi, 11(29), 530-549. Şu adresten erişilebilir:https://doi.org/10.20875/makusobed.595643. Son erişim tarihi: Kasım 2024.
3) Fogarassy, C. (2014). The Interpretation of Sustainability Criteria Using Game Theory Models. Şu adresten erşilebilir: https://real.mtak.hu/23448/1/Fogarassy_Fenntarthatosagi_Rubik_ENG_u.pdf.Son erişim tarihi: Kasım 2024.
4) Game Theory for the Earth. Şu adresten erişilebilir: https://majorsustainability.smeal.psu.edu/concepts/enterprise-risk-management- concepts/gametheoryforearth/. Son erişim tarihi: Eylül 2024.
5) Geeksforgreeks, (2024). Nash Equilibrium. Şu adresten erişilebilir:https://www.geeksforgeeks.org/nash-equilibrium/. Son erişim tarihi: Kasım 2024.
6) Hardin, G. (1968). “The Tragedy of the Commons”, Science162: 1243-1248.
7) Hyman, D. N. (1997). Microeconomics, 4. Baskı, ABD: Irvin Publishing.
8) Kolstad, C. D. (2000). Environmental Economics, New York: Oxford University Press.
9) Major Sustainability. (t.b.) Risk Management and Sustainability. Şu adresten erişilebilir: https://majorsustainability.smeal.psu.edu/concepts/enterprise-risk-management- concepts/gametheoryforearth/. Son erişim tarihi: Kasım 2024.
10) Oyun Teorisi Uygulamaları ve Stratejik Planlama. Şu adresten erişilebilir: https://provega.com.tr/oyun-teorisi-uygulamalari-ve-stratejik-planlama/#:~:text=Oyun%20teorisi,%20matematiksel%20ve%20ekonomik%20bir%20modelleme%20ve%20analiz%20arac%C4%B1d%C4%B1r. Son erişim tarihi: Kasım 2024.
11) Parsons, W. (2005). Public Policy: An Introduction to the Theory and Practice of Policy Analysis, 6. Baskı, Cheltenham-UK: Edward Elgar Publishing Ltd.
12) Polat, M., Akan, Y. (2024). Oyun Teorisi: Strateji ve Karar Mekanizmaları. Şu adresten erişilebilir:https://www.semanticscholar.org/paper/Oyun-Teorisi%3A-Strateji-ve-Karar-Mekanizmalar%C4%B1-Polat Akan/e2f51ef817400790780173f2ae328500edaa97b9#:~:text=Oyun%20teorisi,%20stratejik%20d%C3%BC%C5%9F%C3%BCncenin%20matematiksel%20temellerini%20inceleyen%20bir%20disiplindir.%20Bu. Son erişim tarihi: Kasım 2024.
13) Rosen, H. S. (2005). Public Finance, New York: McGraw-Hill Irvin.
14) Sadik-Zada, E.R. et al. (2024). “Game Theory Applications to Socio-Environmental Studies”, Development Economics, and Sustainability Research, Games2024, 15, 5. Şu adresten erişilebilir: https://doi.org/10.3390/g15010005 . Son erişim tarihi: Kasım 2024.
15) Team Insights Focus, (2024). The Not-So-Odd Relationship Between Game Theory and Sustainability. Şu adresten erişilebilir: https://www.vccircle.com/thenot-so-odd-relationship-between-game-theory-and-sustainability. Son erişim tarihi: Kasım 2024.
16) Uysal, A. (2005). “Nehir Havzalarında Sürdürülebilir Gelişme İçin Bir Yöntem: Oyun Teorisi”. Şu adresten erişilebilir: https://polen.itu.edu.tr/items/b988f899-07e5-4185-b0a1-00708dccc525. Son erişim tarihi: Kasım 2024.
17) Yılmaz, B. (2023). Oyun Teorisi: Stratejik Düşüncenin Matematiksel Temelleri. Şu adresten erişilebilir: https://www.bedriyilmaz.com/bilgi/oyun-teorisi/. Son erişim tarihi: Kasım 2024.

